QR Code has error correction capability to restore data if the code is dirty or damaged. Four error correction levels are available for users to choose according to the operating environment. Raising this level improves error correction capability but also increases the amount of data QR Code size.
To select error correction level, various factors such as the operating environment and QR Code size need to be considered.
Level Q or H may be selected for factory environment where QR Code get dirty, whereas Level L may be selected for clean environment with the large amount of data. Typically, Level M (15%) is most frequently selected.
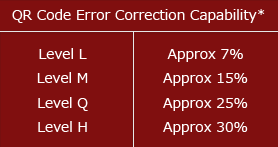
*Data restoration rate for total codewords (codeword is a unit that constructs the data area. One codeword of QR Code is equal to 8 bits.)
Error Correction Feature
The QR Code error correction feature is implemented by adding a Reed-Solomon Code*to the original data.
The error correction capability depends on the amount of data to be corrected. For example, if there are 100 codewords of QR Code to be encoded,50 of which need to be corrected, 100 codewords of Reed-Solomon Code are required, as Reed-Solomon Code requires twice the amount of codewords to be corrected.
In this case, the total codewords are 200, 50 of which can be corrected. Thus, the error correction rate for the total codewords is 25%. This corresponds to QR Code error correction Level Q.
In the example above, the error correction rate for QR Code codewords can be considered as 50%. However, it is not always the case that codewords of not Reed-Solomon Code but only QR Code are susceptible to dirt and damage.QR Code therefore represents its error correction rate as a ratio of the total codewords.
*Reed-Solomon Code is a mathematical error correction method used for music CDs etc. The technology was originally developed as a measure against communication noise for artificial satellites and planetary probes. It is capable of making a correction at the byte level, and is suitable for concentrated burst errors.
